




Fibonacci circles
A lot of shapes and forms that occur in nature follow mathematical rules. The most basic rule is symmetry. This is very clearly visible in early plants and trees like for example the Monkey Puzzle tree that has lived through the time of the dinosaurs. When this tree is young, branches grow in a very symmetrical fashion. Branches are growing on opposite sites on the stem and at the same height. If you would look at the tree from above you would see that the branches each grow side-branches at the same points and on both sides. This gives the tree both bilateral and rotational symmetry. For bilateral symmetry it is easy to think of a butterfly: you can draw an imaginary line through the middle and both sides are the same.

A good example for rotational symmetry is a starfish: rotate the animal just a bit and it looks the same again.

You see that more complex plants and animals diverge from these rules to show more asymmetric forms. This is due to adaptations throughout their evolutionary history, but their primary body structure is still symmetrical. We humans show strong bilateral symmetry as well: we have an arm and a leg on either side, two eyes, two ears, etc. However, the organisation of our organs shows a lot of asymmetries: our heart is somewhat to the left, we have lungs and kidneys on either side, but our liver is on the right and stomach on the left.
Another mathematical rule found widely in nature is the Fibonacci sequence. In this sequence every next number is determined by the sum of the two previous ones.
1 1 2 3 5 8 13 21 34 55 89 144 …
With this sequence you can construct a Fibonacci circle, also called a logarithmic spiral:
Using squares increasing in size according to the Fibonacci sequence a spiral can be constructed that gets wider and wider like in the image from wikipedia below:
This rule determined the way the seeds of a sunflower are organised, and the growth of Romanesco broccoli, which is related to broccoli and cauliflower but has an astonishing structure comprised of a lot of Fibonacci circles made up of larger Fibonacci circles. This process follows another mathematical concept repeatedly found in nature: the fractal.
In the image below I used the Fibonacci sequence to generate a work resulting in a logarithmic spiral.
The version below is constructed using a font that I designed myself, which I named Stark_regular, after my late father-in-law.
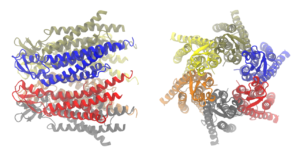
I have always been, and continue to be, fascinated by the structure of proteins. Proteins are large molecules whose structure is encoded in genes and they do most of the work that keeps our cells and us going. On the surface they often look chaotic, but their structures are closely related to and governed by their function. Some proteins have beautifully symmetrical structures, and below is an example of a structure that is actually composed of six separate proteins:
I made my own fantasy protein using the Fibonacci sequence to mimic the initial chaotic appearance of a protein that is actually very symmetrical in its structure.






